本文最后更新于 840 天前,其中的信息可能已经有所发展或是发生改变。
并查集
并查集(Union & find) 是一种树形的数据结构,用于处理一些不交集(Disjoint sets)的合并与查询的问题。初始化时把每个点所在集合初始化为其自身。 Find: 确定元素属于哪一个子集,它可以被用来确定两个元素是否属于同一子集。 Union: 将两个子集合并成同一个子集。
如下图所示,一开始有7个字母,每个都指向自己:

根据某种规则,将相关的字母合并起来,即某个字母会指向另一个字母。假设合并之后是下面的样子:

上图是个树形的结构,左边的集合(a)的根节点为a,它的深度为2,这里树的深度我们称之为秩(rank)。对于这样的树结构,我们如果要合并两个树,可以将秩低的树合并到秩高的树,这样不会增加整个树的秩,如下图所示:
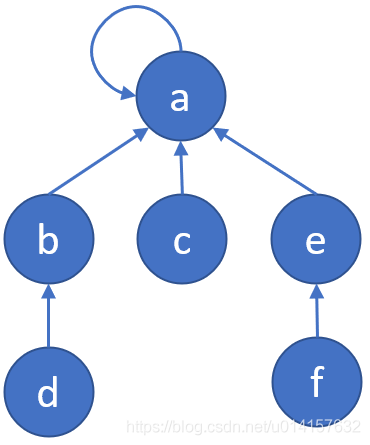
对于并查集,还有一种优化的方式,即路径压缩。我们希望每个节点到根节点的路径尽可能地短,可以将每个节点的父节点设为根节点,比如(a)可以压缩为:
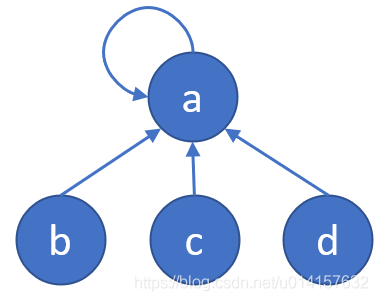
例题
岛屿数量
此题为leetcode第200题此题可以用DFS或BFS解,这两种解法点这里。下面我们用并查集的方法解题。
class UnionFind(object):
def __init__(self, grid):
m, n = len(grid), len(grid[0])
self.count = 0
self.parent = [-1] * (m * n) # 一维数组表示并查集
self.rank = [0] * (m * n)
# 初始化,为1的格子指向自己
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
self.parent[i * n + j] = i * n + j
self.count += 1
# 找根节点
def find(self, i):
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
# 合并
def union(self, x, y):
rootx = self.find(x)
rooty = self.find(y)
if rootx != rooty:
if self.rank[rootx] > self.rank[rooty]: # 低秩合并到高秩
self.parent[rooty] = rootx
elif self.rank[rootx] < self.rank[rooty]:
self.parent[rootx] = rooty
else:
self.parent[rooty] = rootx
self.rank[rootx] += 1
self.count -= 1
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if not grid or len(grid[0]) == 0:
return 0
grid = [[int(i) for i in a] for a in grid] # str-->int
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
uf = UnionFind(grid) # 实例化并查集
m, n = len(grid), len(grid[0])
# 遍历每个元素
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
continue
# 遍历4个方向
for dx, dy in directions:
ii, jj = i + dx, j + dy
# 如果合法的话就合并
if 0 <= ii < m and 0 <= jj < n and grid[ii][jj] == 1:
uf.union(i * n + j, ii * n + jj)
return uf.count朋友圈
此题为leetcode第547题班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
class Solution:
def findCircleNum(self, M: List[List[int]]) -> int:
if len(M) < 2:
return len(M)
if len(M) == 2:
if M[0][1] == 1:
return 1
else:
return 2
n = len(M)
uf = UnionFind(M)
# 只需遍历右上三角即可(不包括对角线)
for i in range(n-1):
for j in range(i+1, n):
if M[i][j] == 1:
uf.union(i, j)
return uf.count
# 并查集
class UnionFind(object):
def __init__(self, M):
n = len(M)
self.count = 0
self.parent = [-1] * n # 一维数组表示并查集
self.rank = [0] * n
# 初始化,为1的格子指向自己
for i in range(n):
self.parent[i] = i
self.count += 1
# 找根节点
def find(self, i):
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
# 合并
def union(self, x, y):
rootx = self.find(x)
rooty = self.find(y)
if rootx != rooty:
if self.rank[rootx] > self.rank[rooty]: # 低秩合并到高秩
self.parent[rooty] = rootx
elif self.rank[rootx] < self.rank[rooty]:
self.parent[rootx] = rooty
else:
self.parent[rooty] = rootx
self.rank[rootx] += 1
self.count -= 1