哈希表

哈希表的原理

哈希表是一种使用哈希函数组织数据，以支持快速插入和搜索的数据结构。哈希表由直接寻址表和哈希函数构成。哈希函数$h(K)$将元素关键字$K$作为自变量，返回元素的存储下标。直接寻址表如下所示：

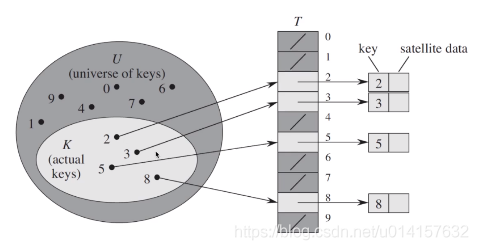
$U$为键值的全域，包含了所有可能的键值，$K$为实际使用的键值，$T$为直接寻址表，每个关键字对应表中的一个位置，比如2、3、5、8这几个关键字对应了$T(2),T(3),T(5),T(8)$。$T(K)$则指向了关键字为$K$的元素。但直接寻址有这样的缺点：

（1）当$U$很大时，需要消耗大量的内存；

（2）若$U$很大而$K$很小，则有很多空间被浪费；

（3）无法处理关键字不是数字的情况。

为改进这些缺点，可以使用哈希函数。直接寻址表是键值为$K$的元素放到$T(K)$位置上，而哈希函数构建一个大小为$m$的寻址表$T$，键值为$K$的元素放到$h(K)$的位置上。$h(K)$是一个函数，将域$U$映射到表$T[0, 1, …, m-1]$。 假设有一个长度为7的哈希表，哈希函数为$h(K)=K%7$。元素集合${14,22,3,5}$的存储方式如下图：

14余7等于0，存在了$T(0)$的位置，22余7等于1，存在了$T(1)$的位置。这样做也会有问题，比如再存一个键值为15的元素，15余7等于1，但此时$T(1)$已经被占了，这就是哈希冲突。如果位置$i$被占，可以解决哈希冲突的方法：

• 线性探查：探查$i+1,i+2,…$这些位置
• 二次探查：$i+1^2, i-1^2, i+2^2, i-2^2,…$这些位置
• 二度哈希：有$n$个哈希函数，当第一个哈希函数冲突时，则使用第二个、第三个……
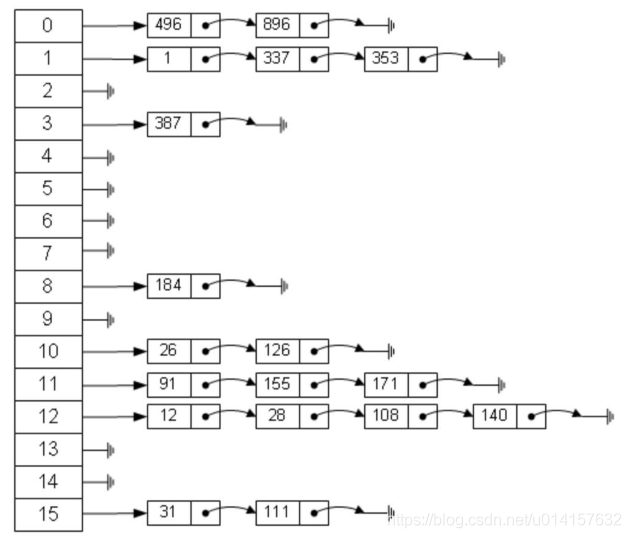
• 拉链法：哈希表每个位置都连一个链表，冲突的元素将被加到该位置链表的最后。如下图所示：

常用的哈希函数：

• 除法哈希：$h(K)=K \% m$
• 乘法哈希：$h(K)=floor(m \times (A * K \% 1))$
• 全域哈希：$h(K)=((a \times K + b) \% p) % m \space \space \space \space a,b=1,2,…p-1$

python里哈希的用法

哈希表由两种不同的类型：哈希集合和哈希映射

• 哈希集合是集合数据结构的实现之一，用于存储非重复值。python里可以用集合set实现：

# 1. 初始化哈希集合
hashset = set() 
# 2. 添加新的键
hashset.add(3)
hashset.add(2)
hashset.add(1)
# 3. 删除键
hashset.remove(2)
# 4. 检查键是否在哈希集合里
if (2 not in hashset):
    print("Key 2 is not in the hash set.")
# 5. 获得哈希集合的大小
print("Size of hashset is:", len(hashset)) 
# 6. 迭代哈希集合
for x in hashset:
    print(x, end=" ")
print("are in the hash set.")
# 7. 清空哈希集合
hashset.clear()
print("Size of hashset:", len(hashset))

• 哈希映射是映射 数据结构的实现之一，用于存储(key, value)键值对。在python可以用字典dict实现：

# 1. 初始化哈希映射
hashmap = {0 : 0, 2 : 3}
# 2. 插入(key, value) 或者更新已存在的键值对
hashmap[1] = 1
hashmap[1] = 2
# 3. 获得键值
print("The value of key 1 is:"  + str(hashmap[1]))
# 4. 删除键
del hashmap[2]
# 5. 检查键是否在哈希集合里
if 2 not in hashmap:
    print("Key 2 is not in the hash map.")
# 6. 键和键值可以有不同的数据类型
hashmap[pi] = 3.1415
# 7. 获得哈希映射的大小
print("The size of hash map is:"  + str(len(hashmap)))
# 8. 迭代哈希映射
for key in hashmap:
    print("(" + str(key) + "," + str(hashmap[key]) + ")", end=" ")
print("are in the hash map.")
# 9. 获得所有键
print(hashmap.keys())
# 10. 清空哈希映射
hashmap.clear();
print("The size of hash map is:"  + str(len(hashmap)))

例题

哈希集合的应用

存在重复元素： 此题为leetcode第217题。

def containsDuplicate(self, nums: List[int]) -> bool:
        hash_ = set()
        for num in nums:
            if num not in hash_:
                hash_.add(num)
            else:
                return True
        return False

• 时间复杂度 : $O(n)$。
• 空间复杂度 : $O(n)$。哈希表占用的空间与元素数量是线性关系。

两个数组的集合： 此题为leetcode第349题

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        set1 = set(nums1)
        set2 = set(nums2)
        return list(set2 & set1)

• 时间复杂度：$O(m+n)$，其中 $n$ 和 $m$ 是数组的长度。$O(n)$ 的时间用于转换 nums1 在集合中，$O(m)$ 的时间用于转换 nums2 到集合中，并且平均情况下，集合的操作为 $O(1)$。 空间复杂度：$O(m+n)$，最坏的情况是数组中的所有元素都不同。

哈希映射的应用

场景一：用映射来提供很多的信息

哈希集合没有映射，只是单一地存储了不同的键。而哈希映射可以将键映射到键值，提供更多的信息。 两数之和： 此题为leetcode第1题

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # 哈希
        hash_ = {}
        for i, a in enumerate(nums):
            b = target - a
            if b in hash_:
                return [i, hash_[b]]
            hash_[a] = i
        return None

• 时间复杂度：$O(n)$，我们只遍历了包含有 $n$ 个元素的列表一次。在表中进行的每次查找只花费 $O(1)$ 的时间。
• 空间复杂度：$O(n)$，所需的额外空间取决于哈希表中存储的元素数量，该表最多需要存储 $n$ 个元素。

三数之和： 此题为leetcode第15题

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        if len(nums) < 3:
            return []
        # 先对数组排序, 遍历数组遇到与前一个元素相同的情况可直接跳过
        nums.sort()
        res = set()
        for i, x in enumerate(nums[:-2]):
            if i >= 1 and nums[i-1] == x:
                continue
            hash_ = {}
            for j, y in enumerate(nums[i+1:]):
                if y not in hash_:
                    hash_[-y-x] = 1
                else:
                    res.add((x, -x - y,  y))
        return list(res)

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

同构字符串： 此题为leetcode第205题

class Solution:
    def isIsomorphic(self, s: str, t: str) -> bool:
        hash_ = {}
        for i, a in enumerate(s):
            if a in hash_:
                if hash_[a] != t[i]:
                    return False
            elif t[i] in hash_.values():
                return False
            else:
                hash_[a] = t[i]
        return True

两个列表的最小索引和： 此题为leetcode第599题

class Solution:
    def findRestaurant(self, list1: List[str], list2: List[str]) -> List[str]:
        hash_ = {}
        temp = len(list1) + len(list2)
        res = []
        for i, a in enumerate(list1):
            hash_[a] = i
        for j, b in enumerate(list2):
            if b in hash_:
                if hash_[b] + j == temp:
                    res.append(b)
                elif hash_[b] + j < temp:
                    res = []
                    res.append(b)
                    temp = hash_[b] + j
        return res

场景二：按键聚合

这类问题是统计键出现的次数，所以对应的键值为该键出现的次数 两个数组的交际II： 此题为leetcode第350题

class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
        hash_ = {}
        res = []
        for num in nums1:
            if num not in hash_:
                hash_[num] = 1
            else:
                hash_[num] += 1
        for num in nums2:
            if num in hash_ and hash_[num] != 0:
                res.append(num)
                hash_[num] -= 1
        return res

• 时间复杂度：$O(n+m)$。其中 $n,m$ 分别代表了数组的大小。 空间复杂度：$O(n)$。如果对较小的数组进行哈希映射使用的空间则为$O(min(n,m))$。

存在重复元素II： 此题为leetcode第219题。解法动画

class Solution:
    def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
        hash_ = set()
        for i, num in enumerate(nums):
            if num not in hash_:
                hash_.add(num)
            else:
                return True
            if len(hash_) > k:
                hash_.remove(nums[i-k])
        return False

• 时间复杂度：$O(n)$。我们会做 $n$ 次搜索、删除、插入 操作，每次操作都耗费常数时间。
• 空间复杂度：$O(min(n,k))$。开辟的额外空间取决于散列表中存储的元素的个数，也就是滑动窗口的大小 $O(min(n,k))$。

设计键

上面的题中，键都是显而易见的，但有时候需要设计合适的键。 字母异位词分组： 此题为leetcode第49题

class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        hash_ = collections.defaultdict(list)
        for str in strs:
            hash_[tuple(sorted(str))].append(str)
        return list(hash_.values())

• 时间复杂度：$O(NKlogK)$，其中 $N$ 是 strs的长度，而 $K$ 是 strs 中字符串的最大长度。当我们遍历每个字符串时，外部循环具有的复杂度为 $O(N)$。然后，我们在 $O(KlogK)$ 的时间内对每个字符串排序。
• 空间复杂度：$O(NK)$，排序存储在 ans 中的全部信息内容。

寻找重复子树： 此题为leetcode第652题

class Solution:
    def findDuplicateSubtrees(self, root: TreeNode) -> List[TreeNode]:
        count = collections.Counter()
        ans = []
        def collect(node):
            if not node: return #
            serial = {},{},{}.format(node.val, collect(node.left), collect(node.right))
            count[serial] += 1
            if count[serial] == 2:
                ans.append(node)
            return serial

        collect(root)
        return ans

• 时间复杂度：$O(N^2)$，其中 $N$ 是二叉树上节点的数量。遍历所有节点，在每个节点处序列化需要时间 $O(N)$。
• 空间复杂度：$O(N^2)$，count 的大小。

设计键总结（参考自leetcode）：

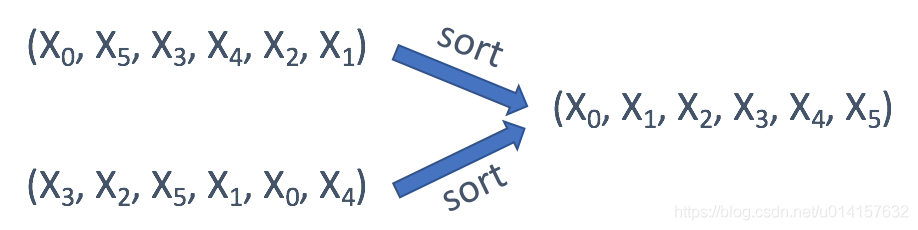
• 当字符串 / 数组中每个元素的顺序不重要时，可以使用排序后的字符串 / 数组作为键：

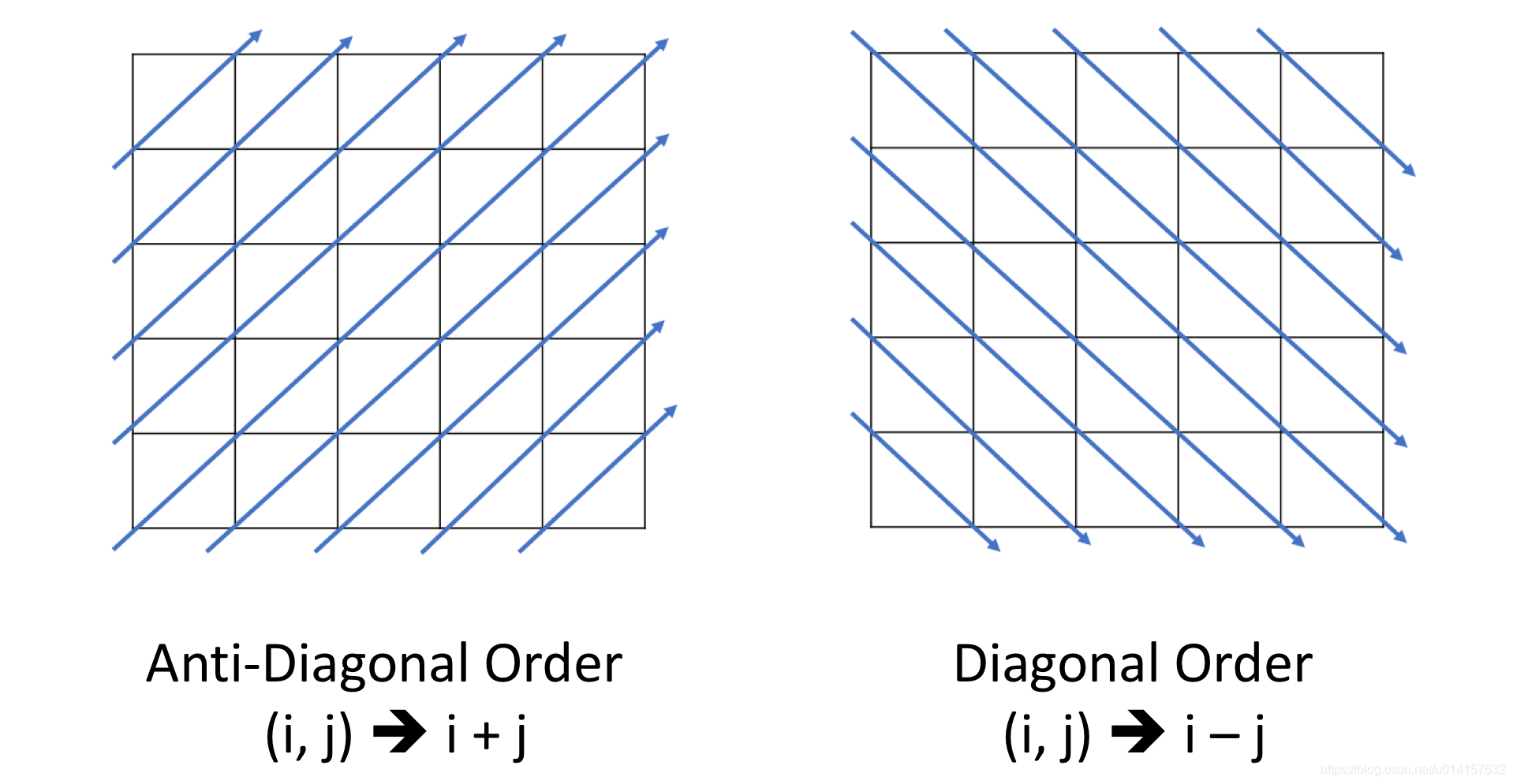
• 如果只关心每个值的偏移量，通常是第一个值的偏移量，则可以使用偏移量作为键：

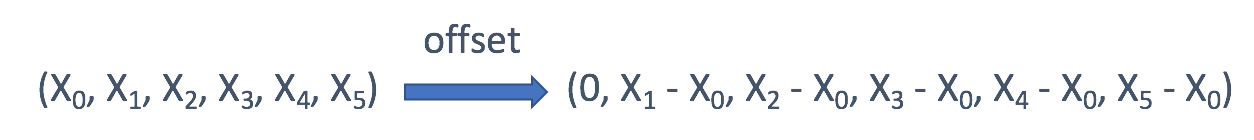
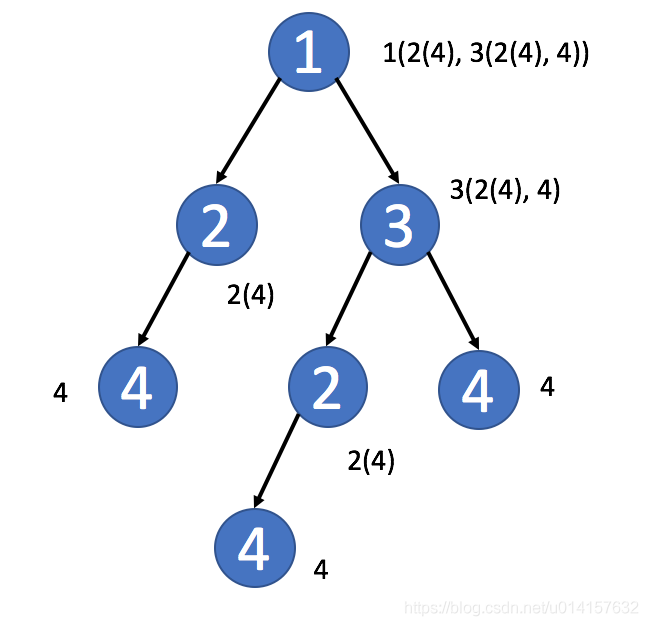
• 在树中，可能会直接使用 TreeNode 作为键。 但在大多数情况下，采用子树的序列化表述可能是一个更好的主意。

• 在矩阵中，可以使用行索引或列索引作为键。

• 在数独中，可以将行索引和列索引组合来标识此元素属于哪个块

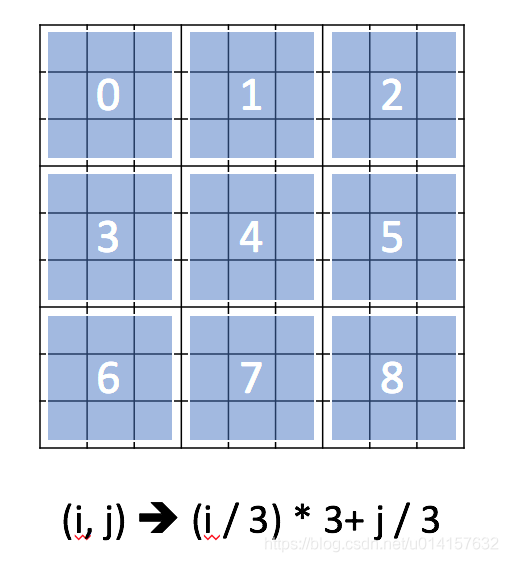
• 有时，在矩阵中，您可能希望将值聚合在同一对角线中