广度优先搜索

广度优先搜索（BFS，Breadth First Search） 的一个常见应用是找出从根结点到目标结点的最短路径，其实现用到了队列。下面用一个例子来说明BFS的原理，在下图中，我们BFS 来找出根结点 A 和目标结点 G 之间的最短路径。

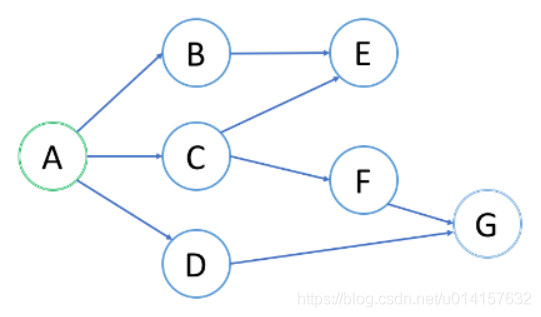
• 首先初始化一个队列Q，将根节点入队：A
• A出队，将与A相邻的节点入队，此时队列为BCD
• B出队，将与B相邻的节点入队，此时队列为CDE
• C出队，将与C相邻的节点入队，此时队列为DEF（节点E已经被遍历过，不需要再入队）
• D出队，将与D相邻的节点入队，此时队列为EFG
• E出队，下面没有节点
• F出队，下面是G，已遍历过，为目标值，遍历结束

BFS代码模板：

def BFS(graph, start, end):
    queue = []
    queue.append([start])
    visited.add(start)  # 对于图来说，要标记节点已经被访问过，防止重复访问

    while queue:
        node = queue.pop()  # 出队
        visited.add(node)   # 标记访问

        process(node)   # 对节点进行一些处理
        nodes = generate_related_nodes(node)    # 得到当前节点的后继节点，并且没有被访问过
        queue.push(nodes)
    # 其他处理部分
    ...

深度优先搜索

与 BFS 类似，深度优先搜索（DFS，Depth-First-Search） 也可用于查找从根结点到目标结点的路径。下面通过一个例子，用DFS 找出从根结点 A 到目标结点 G 的路径。

在上面的例子中，我们从根结点 A 开始。首先，我们选择结点 B的路径，并进行回溯，直到我们到达结点 E，我们无法更进一步深入。然后我们回溯到A并选择第二条路径到结点 C。从 C 开始，我们尝试第一条路径到 E 但是 E已被访问过。所以我们回到 C 并尝试从另一条路径到 F。最后，我们找到了 G。虽然我们成功找出了路径 A-> C-> F-> G ，但这不是从 A 到 G 的最短路径。

DFS代码模板：

# 递归写法
visited = set()
def DFS(node, visited):
    visited.add(node)
    # process current node here
    ...
    for next_node in node.children():
        if next_node not in visited:
            DFS(next_node, visited)

例题

岛屿数量问题

此题为leetcode的第200题。有两个思路：

• Flood fill 算法： 深度优先搜索或广度优先搜索
• 并查集

Flood fill 算法的含义：是从一个区域中提取若干个连通的点与其他相邻区域区分开（或分别染成不同颜色）的经典 算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。在 GNU Go 和 扫雷 中，Flood Fill算法被用来计算需要被清除的区域。

对于这类问题，其实就是从一个点开始，遍历与这个起点连着的格子，遍历过的格子就标上“被访问过”的记号，找到与之相连的所有格子后，就是发现了一个岛屿。而这个遍历的过程可以用广度优先或深度优先实现，具体讲解可以参考这里，动画很明白，这里只贴上代码：

# 广度优先搜索
from typing import List
from collections import deque

class Solution:
    #          x-1,y
    # x,y-1     x, y      x,y+1
    #          x+1,y
    # 方向数组，它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量，这是一个常见的技巧
    directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]

    def numIslands(self, grid: List[List[str]]) -> int:
        m = len(grid)
        if m == 0:
            return 0
        n = len(grid[0])
        marked = [[False for _ in range(n)] for _ in range(m)]
        count = 0
        # 从第 1 行、第 1 格开始，对每一格尝试进行一次 DFS 操作
        for i in range(m):
            for j in range(n):
                # 只要是陆地，且没有被访问过的，就可以使用 BFS 发现与之相连的陆地，并进行标记
                if not marked[i][j] and grid[i][j] == '1':
                    # count 可以理解为连通分量，你可以在广度优先遍历完成以后，再计数，
                    # 即这行代码放在【位置 1】也是可以的
                    count += 1
                    queue = deque()
                    queue.append((i, j))
                    # 注意：这里要标记上已经访问过
                    marked[i][j] = True
                    while queue:
                        cur_x, cur_y = queue.popleft()
                        # 得到 4 个方向的坐标
                        for direction in self.directions:
                            new_i = cur_x + direction[0]
                            new_j = cur_y + direction[1]
                            # 如果不越界、没有被访问过、并且还要是陆地，就入队
                            if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1':
                                queue.append((new_i, new_j))
                                # 入队后马上要标记为“被访问过”
                                marked[new_i][new_j] = True
                    #【位置 1】
        return count

# 深度优先搜索
from typing import List

class Solution:
    #        x-1,y
    # x,y-1    x,y      x,y+1
    #        x+1,y
    # 方向数组，它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量，这是一个常见的技巧
    directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]

    def numIslands(self, grid: List[List[str]]) -> int:
        m = len(grid)
        if m == 0:
            return 0
        n = len(grid[0])
        marked = [[False for _ in range(n)] for _ in range(m)]
        count = 0
        # 从第 1 行、第 1 格开始，对每一格尝试进行一次 DFS 操作
        for i in range(m):
            for j in range(n):
                # 只要是陆地，且没有被访问过的，就可以使用 DFS 发现与之相连的陆地，并进行标记
                if not marked[i][j] and grid[i][j] == '1':
                    # 连通分量计数
                    count += 1
                    # DFS搜索
                    self.__dfs(grid, i, j, m, n, marked)
        return count

    # 递归进行深度优先搜索
    def __dfs(self, grid, i, j, m, n, marked):
        marked[i][j] = True
        for direction in self.directions:
            new_i = i + direction[0]
            new_j = j + direction[1]
            if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1':
                self.__dfs(grid, new_i, new_j, m, n, marked)

二叉树的最大深度

此题为leetcode第104题
给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

深度优先解法：

# 深度优先搜索
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        # 递归，深度优先搜索
        if root is None: 
            return 0 
        else: 
            left_height = self.maxDepth(root.left)    # 左子树高度
            right_height = self.maxDepth(root.right)  # 右子树高度
            return max(left_height, right_height) + 1 

广度优先解法：

# 迭代，广度优先搜索
from collections import deque
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0

        depth = 0
        q = deque()
        q.append((1, root))
        while q:
            curr_depth, node = q.pop()
            depth = max(depth, curr_depth)

            if node.left:
                q.append((curr_depth + 1, node.left))
            if node.right:
                q.append((curr_depth + 1, node.right))
        return depth

二叉树的最小深度

此题为leetcode第111题
给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

深度优先解法：

# 递归，深度优先搜索
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        # 递归，深度优先搜索
        if root is None: 
            return 0 
        if root.left is None:   # 若左子树为空，root的深度为1+右子树深度
            return 1 + self.minDepth(root.right)
        if root.right is None:  # 若右子树为空，root的深入为1+左子树深度
            return 1 + self.minDepth(root.left)

        left_height = self.minDepth(root.left)    # 左子树高度
        right_height = self.minDepth(root.right)  # 右子树高度

        return min(left_height, right_height) + 1 

广度优先解法：

# 迭代，广度优先搜索
from collections import deque
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        # 迭代，广度优先搜索
        if root is None:
            return 0

        q = deque()
        q.append((1, root))
        depth = 1
        while q:
            curr_depth, node = q.popleft()
            # 如果node为叶子节点，则此时深度为最小深度
            if node.left is None and node.right is None:
                return curr_depth

            if node.left:
                q.append((curr_depth + 1, node.left))
            if node.right:
                q.append((curr_depth + 1, node.right))

括号生成

此题为leetcode第22题
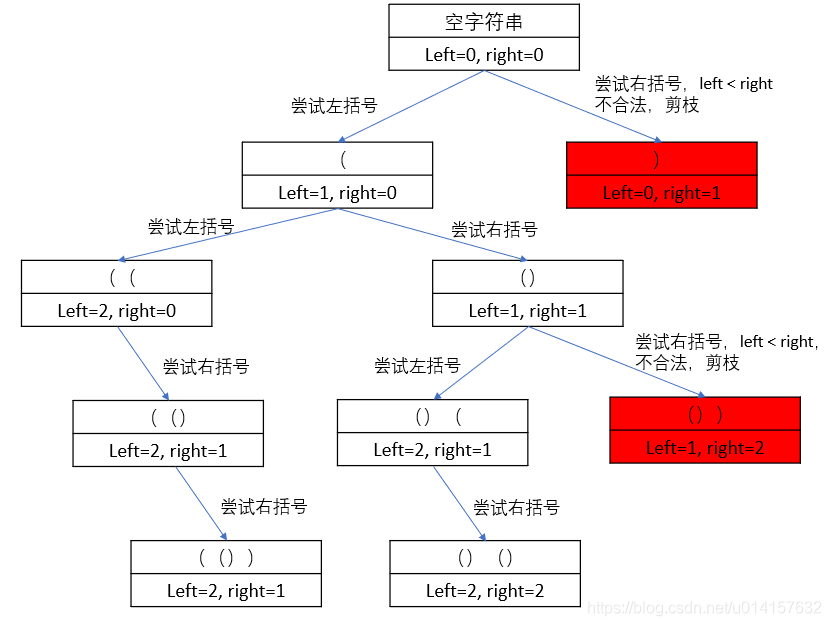
思路：可以使用深度优先搜索，尝试每种组合方式，但搜索的个数会是指数级的，因此需要考虑剪枝，有些组合一开始不合法，后面的肯定也不合法。什么情况下是不合法的呢，当尝试右括号时，除去已经配好对的括号，如果这个右括号没有与之配对的左括号，那它就是不合法的，后面的组合肯定也是不合法的。我们可以定义两个计数变量left和right，表示左右括号还有几个没用。如果left > right，说明右括号被用后没有与之配对的左括号，为不合法组合。

# 深度优先搜索加剪枝
class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        self.res = []
        self._gen('', 0, 0, n)
        return self.res

    def _gen(self, result, left, right, n):
        # left为左括号用了几个，right为右括号用了几个
        if left == n and right == n:
            self.res.append(result)
            return 

        # 如果用的左括号小于n个，可以加左括号
        if left < n:
            self._gen(result+'(', left+1, right, n)
        # 只有在用的右括号小于用的左括号时，才可以加右括号
        if right < left:
            self._gen(result+')', left, right+1, n)

N皇后问题

此题为leetcode第51题
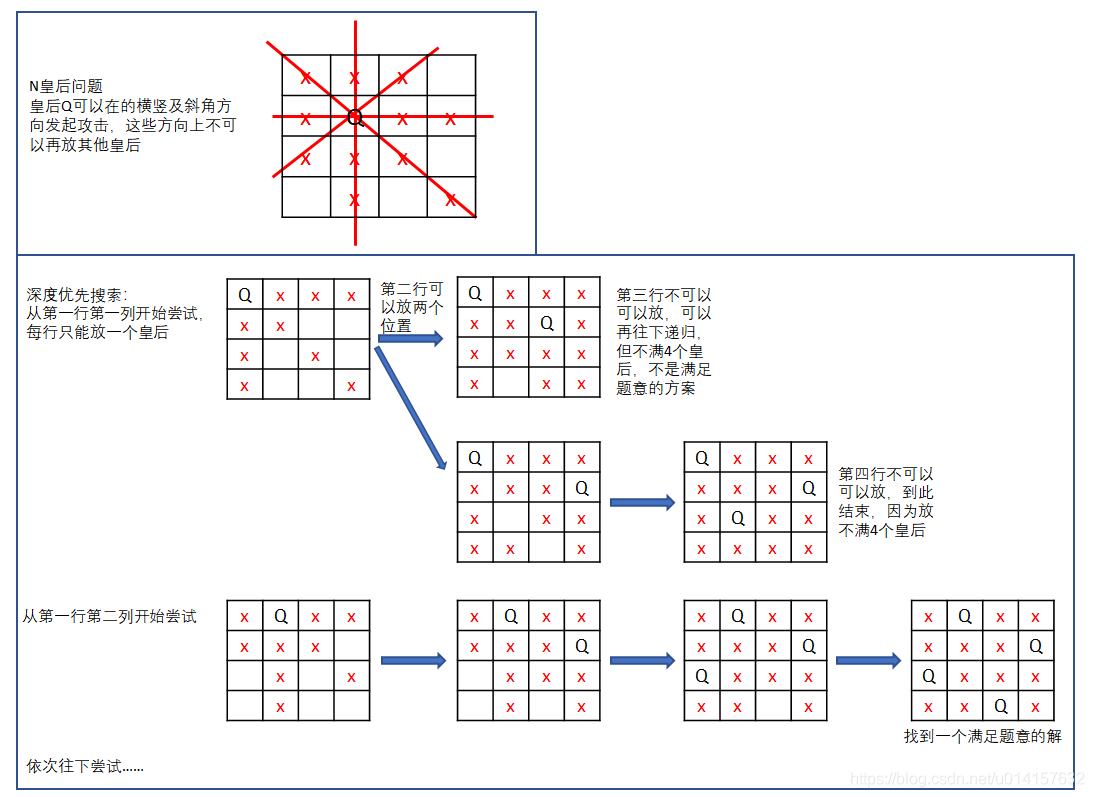
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 \’Q\’ 和 \’.\’ 分别代表了皇后和空位。

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        if n < 1:
            return []
        self.res = []   # 记录最终结果
        self.cols, self.pie, self.na = set(), set(), set()  # 标记横竖、斜角方向
        self.DFS(n, 0, [])

        return [['.' * j + 'Q' + '.' * (n - j - 1) for j in col] for col in self.res]

    def DFS(self, n, row, curr_state):  # curr_state代表每行的哪些列可以放置皇后，是一种可能的解决方案
        # 如果递归可以走到最后一层，说明curr_state是一种合法的解决方案，将其放入self.res里
        if row >= n:
            self.res.append(curr_state)
            return

        # 遍历列
        for col in range(n):
            # 如果当前位置上，可以被横竖、斜角方向上的皇后攻击到，则continue
            if col in self.cols or row + col in self.pie or row - col in self.na:
                continue  

            # 如果当前位置不会被攻击到，则标记横竖、斜角方向
            self.cols.add(col)
            self.pie.add(row + col)
            self.na.add(row - col)

            # 递归，row+1进入下一行，curr_state+[col]保存一种可能的状态
            self.DFS(n, row + 1, curr_state + [col])

            # 上面的递归出来后，清除横竖、斜角方向的标记
            # 因为我们是在(n, col)位置上尝试放置皇后看是否可行
            self.cols.remove(col)
            self.pie.remove(row + col)
            self.na.remove(row - col)

解数独

此题为leetcode第37题
编写一个程序，通过已填充的空格来解决数独问题。下面给出最朴素的DFS：

class Solution:
    def solveSudoku(self, board: List[List[str]]) -> None:
        '''
        Do not return anything, modify board in-place instead.
        '''
        if board is None or len(board) == 0:
            return
        self.solve(board)

    def solve(self, board):
        for i in range(len(board)):
            for j in range(len(board)):
                # 循环遍历，找到空位置
                if board[i][j] == '.':
                    # 从1-9遍历
                    for k in range(1, 10):
                        c = str(k)
                        if self.isValid(board, i, j, c):    # 判断c是否可以放在(i, j)上
                            # 如果在(i, j)上放数字c可行的话，先将c放上去
                            board[i][j] = c
                            # 继续递归，看放上c后，后面的是否可行
                            if self.solve(board):
                                return True     # 放上c后可以解决整个数独则返回True
                            else:
                                board[i][j] = '.'   # 不可行的话将c清空
                    return False    # 1-9遍历完后还不行就返回False
        return True    # 可以遍历完整个board就返回True

    def isValid(self, board, row, col, c):
        for i in range(9):
            if board[i][col] != '.' and board[i][col] == c:
                return False
            if board[row][i] != '.' and board[row][i] == c:
                return False
            if board[3 * (row // 3) + i // 3][3 * (col // 3) + i % 3] != '.' and board[3 * (row // 3) + i // 3][3 * (col // 3) + i % 3] == c:
                return False
        return True