平衡二叉树

什么是平衡二叉树： 每个节点的两个子树的高度不会相差超过1。普通树和平衡二叉树的对比：

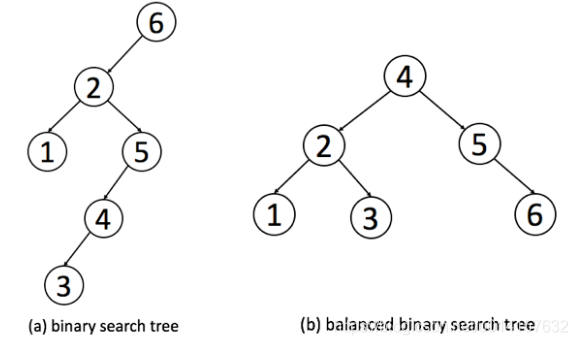
为什么要用到平衡二叉树： 在二叉搜索树里面，搜索操作的时间复杂度从$O(logN)$到$O(N)$不等，这是一个巨大的性能差异。而平衡的二叉搜索树的搜索复杂度为$O(logN)$。 常见的平衡二叉树的实现： 红黑树、AVL树、伸展树、树堆

判断是否为平衡二叉树

自底至顶递归： 做先序遍历，从底部开始，判断左右子树高度差，若是平衡二叉树则返回子树的最大高度，若不是则直接输出false。 此题为leetcode第110题，代码如下：

class Solution:
    def recur(self, root):
        # 越过叶子节点，返回高度0
        if not root: 
            return 0

        left = self.recur(root.left)
        if left == -1: 
            return -1

        right = self.recur(root.right)
        if right == -1: 
            return -1
        # 如果高度差大于1则不是平衡二叉树，否则返回左右子树最大高度加1
        return max(left, right) + 1 if abs(left - right) < 2 else -1

    def isBalanced(self, root: TreeNode) -> bool:
        return self.recur(root) != -1

复杂度分析：

• 时间复杂度：$O(N)$，N 为树的节点数；最差情况下，需要递归遍历树的所有节点。
• 空间复杂度：$O(N)$，最差情况下（树退化为链表时），系统递归需要使用 $O(N)$ 的栈空间。