优先队列

优先队列按照队列的方式正常入队，但按照优先级出队。有两种实现方式：堆（二插堆、多项式堆等等）和二叉搜索树。这里重点讲解二叉堆，关于二叉搜索树的内容见这篇文章。

堆是一种特殊的完全二叉树。大根堆： 完全二叉树的任一节点都比其孩子节点大。小根堆： 完全二叉树的任一节点都比其孩子节点小。堆的向下调整： 假设根节点的左右子树都是堆，但根节点不满足堆的性质，可以通过一次向下调整将其变成一个堆。因为二叉堆是完全二叉树，一般可以用数组来表示，这样不会浪费空间。大根堆和小根堆的举例如下所示：

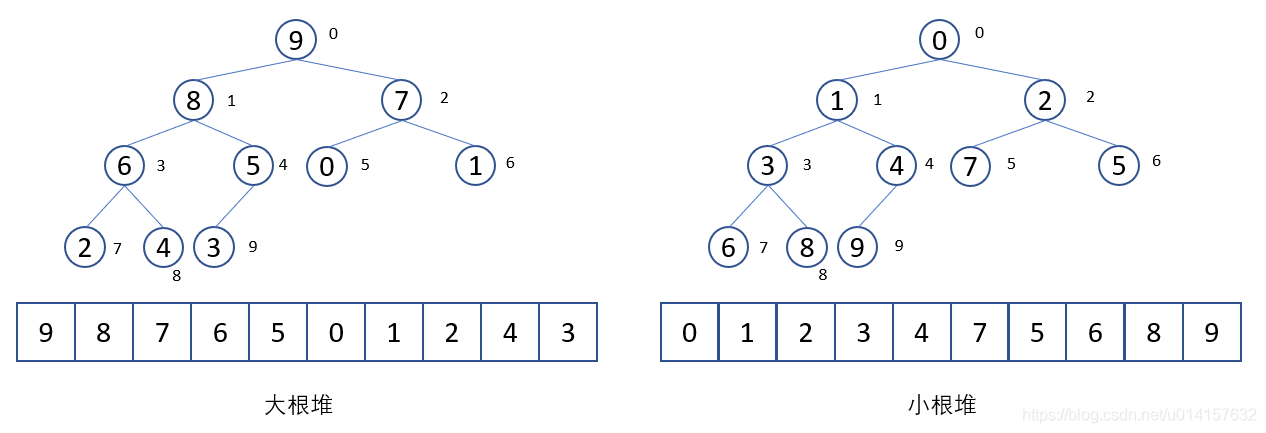
用数组表示的二叉堆，有如下性质：

• 第$i$个节点的左孩子的下标为$2 \times i + 1$，右孩子的下标为$2 \times i + 2$。
• 第$i$个节点的父亲节点的下标为$(i-1)//2$

二叉堆的时间复杂度：

• 插入操作：$O(\log n)$
• 删除操作：$O(\log n)$
• 查询最小值：$O(1)$

python实现：heapq

import heapq

# 将array列表转为堆的结构
heap.heapify(array)
# 弹出堆中的最小值
heapq.heappop(array)
# 往堆中插入新值a
heapq.heappush(array, a)
# 先进行heappop(array)，再进行heappush(array, a)操作
heapq.heapreplace(array, a)
# 获得array中前k个最大的值
heapq.nlargest(k, array)
# 获得array中前k个最小的值
heapq.nsmallest(k, array)

例题

合并k个有序链表

此题为leetcode第23题合并 k 个排序链表，返回合并后的排序链表。

import heapq
class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        head = p = ListNode(0)
        # 建立堆
        a = []
        for i in range(len(lists)):
            if lists[i] :
                # 元组在heapq里比较的机制是从元组首位0开始，即遇到相同，就比较元组下一位
                # 比如(1,2), (1,3)，前者比后者小。
                # 这题刚好node值有重复的，同时ListNode无法被比较，所以会报错
                heapq.heappush(a, (lists[i].val, i))
                lists[i] = lists[i].next
        while a:
            val, idx = heapq.heappop(a)
            p.next = ListNode(val)
            p = p.next
            if lists[idx]:
                heapq.heappush(a, (lists[idx].val, idx))
                lists[idx] = lists[idx].next
        return head.next

• 时间复杂度：$O(n \log k)$
• 空间复杂度：$O(k+n)$，最小堆需要k个空间，新链表需要n个空间

数据流中的第k大元素

此题为leetcode第703题设计一个找到数据流中第K大元素的类（class）。注意是排序后的第K大元素，不是第K个不同的元素。你的 KthLargest 类需要一个同时接收整数 k 和整数数组nums 的构造器，它包含数据流中的初始元素。每次调用 KthLargest.add，返回当前数据流中第K大的元素。

import heapq
class KthLargest:
    def __init__(self, k: int, nums: List[int]):
        self.nums = nums
        self.k = k
        heapq.heapify(self.nums)
        # 留下k个元素，即前k大的
        while len(self.nums) > k:
            heapq.heappop(self.nums)

    def add(self, val: int) -> int:
        if len(self.nums) < self.k:
            heapq.heappush(self.nums, val)
        elif self.nums[0] < val:
            # 新的值更大则更新
            heapq.heapreplace(self.nums, val)

        return self.nums[0]