二叉搜索树

二叉搜索树（BST）满足的性质：

• 每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
• 每个节点中的值必须小于（或等于）存储在其右子树中的任何值。

一个二叉搜索树的例子如下所示：

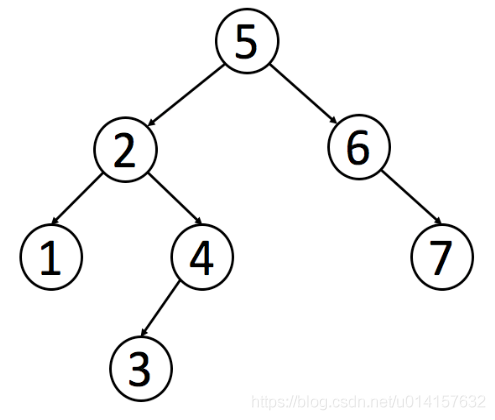
因为二叉树的中序遍历会得到一个递增的序列，因此在二叉搜索树里中序遍历比较常用。

给定一个二叉树，我们要判断它是否是二叉搜索树。二叉搜索树的特征比较明显，我们需要判断：（1）当前节点下，其左子树只包含小于当前节点的数；（2）其右子树只包含大于当前节点的数；（3）所有左子树右子树必须也是二叉搜索树。此题是leetcode的第98题，我们用递归、迭代、中序遍历三种方法实现。

【注意】直观来看，遍历每个节点，只要当前节点比左节点大比右节点小就行。但这样是不对的，因为我们还要右子树的所有节点都要比当前节点大，左子树的所有节点都要比当前节点小，刚才的做法无法保证这一点。比如下图，虽然根节点5小于右节点6，但右子树有个节点值为4，小于根节点，因此不是二叉搜索树。

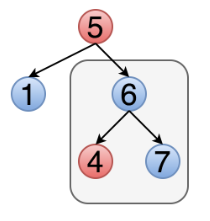
这种情况下，在右子树里比较时，要有一个下界，这个子树里的值都不能小于这个下界，这个下界就是根节点的值。同理，根节点的值就是左子树的上界，所有值都不能大于这个上界。

递归

# 递归判断是否为二叉搜索树
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        # 上界初始化为无穷，下界初始化为负无穷
        def helper(node, lower = float('-inf'), upper = float('inf')):
            if not node:
                return True

            val = node.val
            # 如果当前节点小于下界或大于上界，则不是BST
            if val <= lower or val >= upper:    
                return False
            # 考察右子树是否有低于下界的
            if not helper(node.right, val, upper):
                return False
            # 考察左子树是否有高于上界的
            if not helper(node.left, lower, val):
                return False
            # 以上都满足，则是BST
            return True

        return helper(root)

复杂度分析：

• 时间复杂度：$O(N)$，每个节点访问了一次
• 空间复杂度：$O(N)$，跟进了整个树

迭代

# 迭代法，深度优先搜索
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        if not root:
            return True
        # 初始化栈
        stack = [(root, float('-inf'), float('inf')), ] 
        while stack:
            # 出栈
            root, lower, upper = stack.pop()
            # 如果not root，说明此节点的父节点没有左孩子或右孩子，continue即可
            if not root:
                continue

            val = root.val
            # 判断当前节点
            if val <= lower or val >= upper:
                return False
            # 压栈右孩子
            stack.append((root.right, val, upper))
            # 压栈左孩子
            stack.append((root.left, lower, val))
        return True 

复杂度分析：

• 时间复杂度：$O(N)$，每个节点访问了一次
• 空间复杂度：$O(N)$，跟进了整个树

中序遍历

# 中序遍历
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        stack, inorder = [], float('-inf')

        while stack or root:
            # 到最左边的叶子节点
            while root:
                stack.append(root)
                root = root.left
            # 出栈
            root = stack.pop()
            # 如果它小于它前一个节点的值，则不是BST（因为是中序遍历，是按照递增排的）
            if root.val <= inorder:
                return False
            # 若它大于前一个值，则将当前值赋值给inorder值
            inorder = root.val
            root = root.right

        return True

复杂度分析：

• 时间复杂度：时间复杂度 : 最坏情况下（树为二叉搜索树或破坏条件的元素是最右叶结点）为$O(N)$
• 空间复杂度：$O(N)$用于存储stack

二、基本操作

在树中搜索某个值

在搜索二叉树中找到某个值并返回改节点，举例如下图所示。我们要找到值为4的节点，从根节点开始，它大于4，因此在左子树找。左子树的根节点小于4，因此再在其右子树找。此时当前节点值为4，返回该节点。此题对于leetcode的第700题。

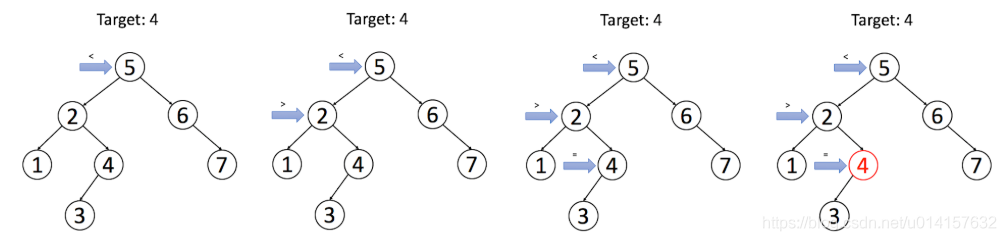
递归实现

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        # 如果给节点为空，或该节点值等于要找到的值，则返回改节点
        if not root or root.val == val:
            return root
        # 若改节点值大于val，则在左子树找
        if root.val > val:
            return self.searchBST(root.left,val)
        # 否则在右子树找
        else:
            return self.searchBST(root.right,val)

复杂度分析：

• 时间复杂度：$O(H)$，其中H是树高。平均时间复杂度：$O(\log N)$；最坏时间复杂度：$O(N)$
• 空间复杂度：$O(H)$，递归栈的深度为H。平均情况下深度为$O(\log N)$；最坏情况戏曲深度为$O(N)$

迭代实现

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root is not None and root.val != val:
            root = root.left if val < root.val else root.right
        return root

复杂度分析：

• 时间复杂度：$O(H)$，其中H是树高。平均时间复杂度：$O(\log N)$；最坏时间复杂度：$O(N)$
• 空间复杂度：$O(1)$，恒定的额外空间

插入操作

在这里实现的二叉搜索树的插入操作，主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。举例如下图所示：

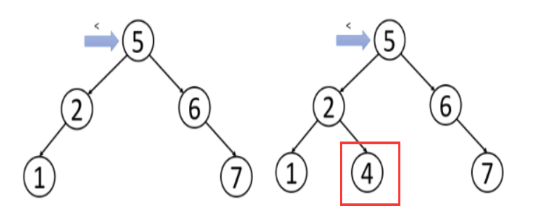
在左边这个树里插入4，从根节点开始，4小于5，因此继续搜索左子树。4大于2，而且2没有右孩子，因此4作为2的右孩子插入到树中。此题对于leetcode的第701题。

递归实现：

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return TreeNode(val)

        if val > root.val:
            # 在右子树插入
            root.right = self.insertIntoBST(root.right, val)
        else:
            # 在左子树插入
            root.left = self.insertIntoBST(root.left, val)
        return root

复杂度分析：

• 时间复杂度：$O(H)$，其中H是树高。平均时间复杂度：$O(\log N)$；最坏时间复杂度：$O(N)$
• 空间复杂度：平均情况下 $O(H)$。最坏的情况下是 $O(N)$，是在递归过程中堆栈使用的空间。

迭代实现：

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        node = root
        while node:
            # 如果val大于当前节点的值，则在右子树插入
            if val > node.val:
                # 如果没有右孩子，则插入
                if not node.right:
                    node.right = TreeNode(val)
                    return root
                else:
                    node = node.right
            # 如果val大于当前节点的值，则在左子树插入
            else:
                # 如果没有左孩子，则插入
                if not node.left:
                    node.left = TreeNode(val)
                    return root
                else:
                    node = node.left
        return TreeNode(val)

复杂度分析：

• 时间复杂度：$O(H)$，其中H是树高。平均时间复杂度：$O(\log N)$；最坏时间复杂度：$O(N)$。
• 空间复杂度：$O(1)$

删除操作

这里的删除操作是用一个合适的子节点来替换要删除的目标节点，使整体操作变化最小。如果目标节点值大于当前节点，则指向右子树去寻找目标节点；如果目标节点值小于当前节点，则指向左子树去寻找目标节点。如果找到了目标节点，我们分为三种情况：

• case1：目标节点没有子节点，可以直接删除目标节点。如下图所示：

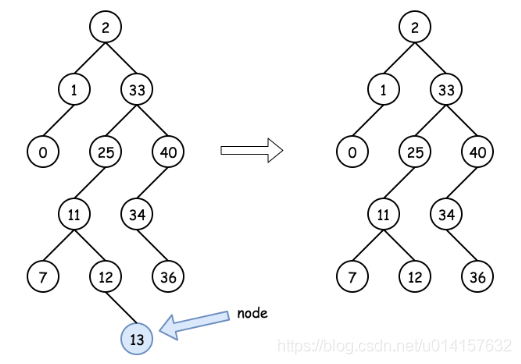
• case2：目标节点有右节点，则该节点可以由该节点的后继节点（successor，右子树最左边的节点）进行替代，该后继节点位于右子树中较低的位置。然后可以从后继节点的位置递归向下操作以删除后继节点。如下图所示：

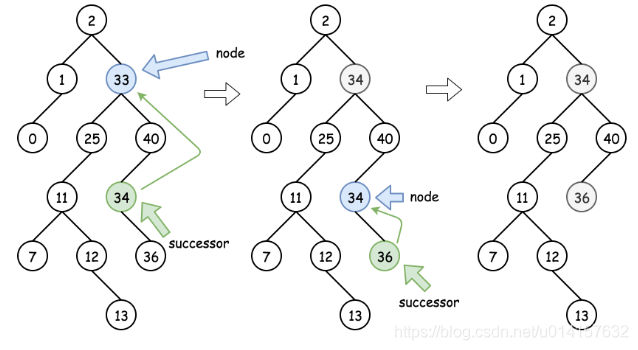
• case3：目标节点只有左节点，可以使用它的前驱节点（predecessor，左子树最右边的节点）进行替代，然后再递归的向下删除前驱节点。如下图所示：

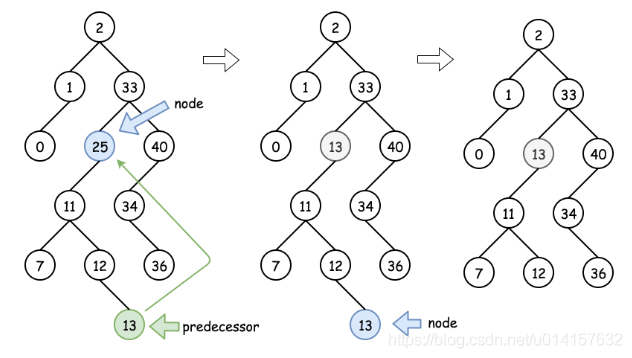
此题对于leetcode的第450题。代码如下：

class Solution:
    def successor(self, root):
        # 最左边的节点
        root = root.right
        while root.left:
            root = root.left
        return root.val

    def predecessor(self, root):
        # 最右边的节点
        root = root.left
        while root.right:
            root = root.right
        return root.val

    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None

        # 从右子树删除
        if key > root.val:
            root.right = self.deleteNode(root.right, key)
        # 从左子树删除
        elif key < root.val:
            root.left = self.deleteNode(root.left, key)
        # 找到了要删除的节点
        else:
            # case 1
            if not (root.left or root.right):
                root = None
            # case 2
            elif root.right:
                root.val = self.successor(root)
                root.right = self.deleteNode(root.right, root.val)
            # case 3
            else:
                root.val = self.predecessor(root)
                root.left = self.deleteNode(root.left, root.val)

        return root

复杂度分析：

• 时间复杂度：时间复杂度：${O}(\log N)$。在算法的执行过程中，我们一直在树上向左或向右移动。首先先用$O(H_1)$的时间找到要删除的节点，$H_1$是从根节点到要删除节点的高度。然后删除节点需要 ${O}(H_2)$的时间，$H_2$指的是从要删除节点到替换节点的高度。由于 ${O}(H_1 + H_2) = {O}(H)$，$H$ 值得是树的高度，若树是一个平衡树则 $H = \log N$。
• 空间复杂度：空间复杂度：$O(H)$，递归时堆栈使用的空间，H 是树的高度

例题

二叉搜索树的最近公共祖先

此题为leetcode第235题给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

递归写法：

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 递归
        # 当p、q的值都小于root时，要在左子树找
        if p.val < root.val and q.val < root.val:
            return self.lowestCommonAncestor(root.left, p, q)
        # 当p、q的值都大于root时，要在右子树找
        if p.val > root.val and q.val > root.val:
            return self.lowestCommonAncestor(root.right, p, q)
        # 否则p或q分列左右子树，root即为最近公共祖先
        return root

非递归写法：

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 非递归
        while root:
            if p.val < root.val and q.val < root.val:
                root = root.left
            elif p.val > root.val and q.val > root.val:
                root = root.right
            else:
                return root