本文最后更新于 395 天前，其中的信息可能已经有所发展或是发生改变。

二叉树

二叉树是一种更为典型的树树状结构。如它名字所描述的那样，二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。下面是个二叉树的例子：

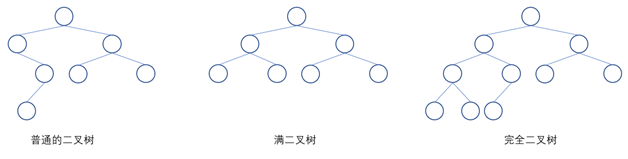
用python定义二叉树的节点：

# 二叉树节点
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

二叉树遍历

前序遍历

前序遍历访问的顺序为：根节点、左子树、右子树。对于上图，遍历过程如下：

一开始指向根节点，访问它，为E
有左子树，指向他并访问，为A
A没有左子树，指向其右子树并访问，为C
C有左子树和右子树，按顺序访问，为BD
E的左半边访问完毕，指向E的右子树并访问，为G
G只有右子树，访问它，为F
F往下已经没有叶子节点，遍历结束

因此，前序遍历的结果为：EACBDGF

中序遍历

中序遍历访问的顺序为：左子树、根节点、右子树。对于上图，遍历过程如下：

一开始指向根节点E，因为优先访问左子树，先看有没有左子树。发现根节点有左子树A，指向它
此时A有没有左子树，因此访问当前节点，为A
A有右子树，指向其右子树C
此节点C有左子树，指向其左子树B
此时节点没有子树，访问其节点为B
然后往回指向节点B的父节点，并访问，为C
C有右子树，访问，为D
此时指回根节点E，访问它，为E
E有右子树，指向右子树G
因为G没有左子树，因此访问当前节点，为G
G有右子树，访问，为F
F无子树，遍历结束

因此，中序遍历的结果为：ABCDEGF。通常来说，对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列

后序遍历

后序遍历访问的顺序为：左子树、右子树、根节点。对于上图，遍历过程如下：

一开始指向根节点E，先指向左子树A
要优先访问左子树右子树，A无左子树、有右子树，因此指向A的右子树C
C有左子树，指向左子树B
B无子树，访问为B
指回C，C有右子树，指向并访问，为D
指回BD的根节点C，访问为C
指回C的根节点，访问为A
指回A的根节点E，访问其右子树G
G有右子树，访问为F
指回F的根节点，访问为G
指回G的根节点，访问为E
E已为整个树的根节点，遍历结束

因此，后序遍历的结果为：BDCAFGE。当你删除树中的节点时，用到后序遍历。也就是说，当你删除一个节点时，你将首先删除它的左节点和它的右边的节点，然后再删除节点本身。

层序遍历

层序遍历就是逐层遍历树结构，下图展示了它的层次结构：

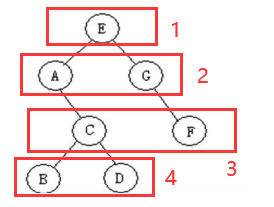
二叉树的层序遍历即为广度优先搜索，该算法从一个根节点开始，首先访问节点本身。然后遍历它的相邻节点，其次遍历它的二级邻节点、三级邻节点，以此类推。广度优先搜索需要用到队列。遍历过程如下：

初始化队列q=[]，并将根节点E入队，为q=[E]
q出队，为E
E有左子树和右子树，两者入队，为q=[A, G]
q出队，为A，此时将A的右子树入队，为q=[G, C]
q出队，为G，此时G的右子树入队，为q=[C, F]
q出队，为C，此时C的左子树、右子树入队，为q=[F, B, D]
q出队，为F，此时q=[B, D]
F没有子树，q继续出队，为B，此时q=[D]
q出队，为D
q为空，遍历结束

因此，层序遍历的结果为：EAGCFBD。

程序实现

二叉树的前序、中序、后序和层序遍历，分别为leetcode的第144、94、145、102题，都可以用递归和迭代两种方法做。

递归实现

对于前序、中序和后序来说，递归的现实非常简单，他们的实现区别是根节点访问的顺序不一样。代码如下：

# 前序遍历递归
class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        else:
            return [root.val] + self.preorderTraversal(root.left) + self.preorderTraversal(root.right)

# 中序遍历递归
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        else:
            return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)

# 后序遍历递归
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        else:
            return self.postorderTraversal(root.left)  + self.postorderTraversal(root.right)+ [root.val]

可以看出不同的地方就是[root.val]的位置不一样，前序遍历[root.val]就在最一开始，中序遍历[root.val]则在中间，后序遍历[root.val]就在最后。整个迭代结构下图所示：

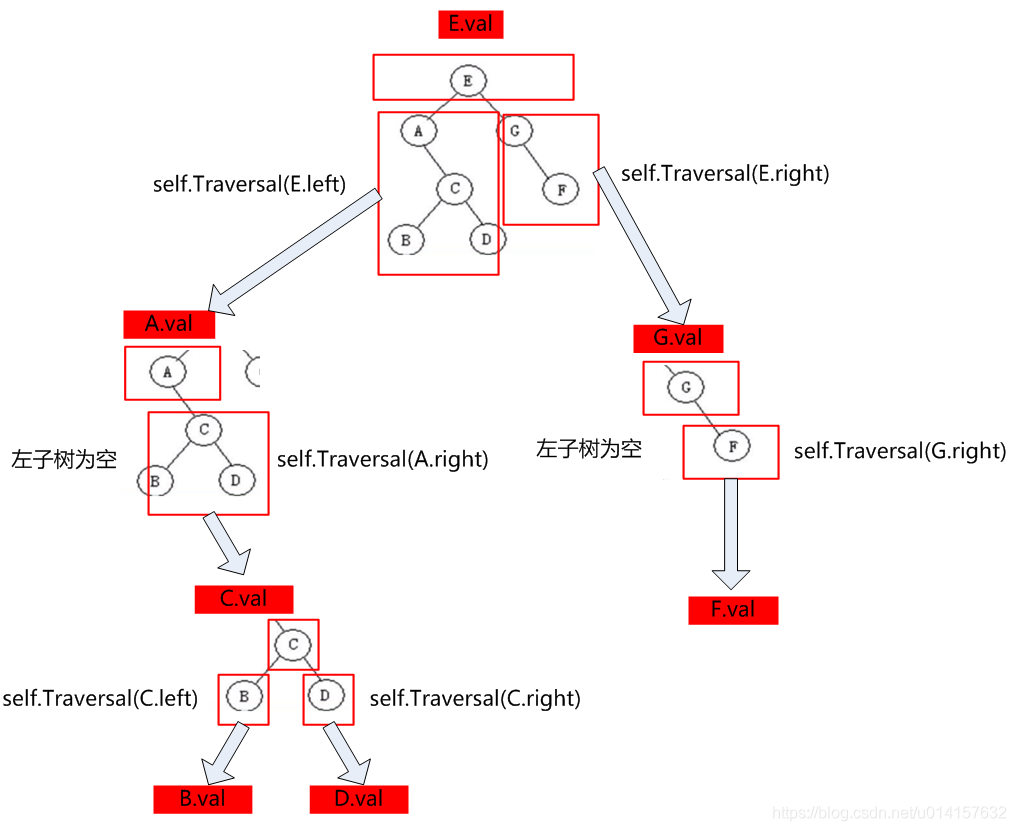
对于层序遍历的递归实现，我们不仅要输出层序遍历的序列，还要有每个元素属于哪个层次的信息，可以用列表嵌套的方式，比如之前的例子里，层序遍历表示为[[E], [AG], [CF], [BD]]。

# 层序遍历递归
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        levels = []
        if not root:
            return levels

        def helper(node, level):
            # start the current level
            if len(levels) == level:
                levels.append([])

            # append the current node value
            levels[level].append(node.val)

            # process child nodes for the next level
            if node.left:
                helper(node.left, level + 1)
            if node.right:
                helper(node.right, level + 1)

        helper(root, 0)
        return levels

我们设更节点的层级序号为0，依次往下为1、2、3……。leaves为保存结果的列表，每一层的结果又为一个列表，保存在leaves里，层级序号即为在leaves里的index，在第i层级，leaves里应该有i+1个列表，第i+1个列表为当前层级的节点。每个列表只append层级序号相同的节点。

迭代实现

二叉树的迭代实现都需要用到栈。对于前序、中序、后序遍历，他们的迭代实现大同小异：

# 前序遍历迭代
class Solution:        
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if root is None:
            return []

        stack, output = [root, ], []
        while stack:
            root = stack.pop()
            if root is not None:
                output.append(root.val)
                if root.right is not None:
                    stack.append(root.right)
                if root.left is not None:
                    stack.append(root.left)

        return output

# 中序遍历迭代
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        if root is None:
            return []

        stack, output= [], []
        curr = root
        while curr or len(stack) > 0:
            while curr:
                stack.append(curr)
                curr = curr.left
            curr = stack.pop()
            output.append(curr.val)
            curr = curr.right
        return output

# 后序遍历迭代
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        if root is None:
            return []

        stack, output = [root, ], []
        while stack:
            root = stack.pop()
            output.append(root.val)
            if root.left is not None:
                stack.append(root.left)
            if root.right is not None:
                stack.append(root.right)

        return output[::-1]

对于前序遍历，先初始化一个有根节点的栈，然后进入循环，出栈根节点，访问它。然后依次入栈右子树、左子树（注意栈是先进后出）。则下次循环，会先出栈左子树，访问它，然后入栈它的右子树、左子树。这样根节点E的右子树会在其左子树遍历完后才会出栈。循环停止条件是栈为空。
对于中序遍历，因为要优先遍历左子树，循环之前初始化一个空栈，进入循环后，用一个内循环依次入栈左子树，直到叶子节点（也为一个左子树），然后退出内循环，出栈并访问。
对于后序遍历，和前序遍历的整体结构是一样的，唯一不同的是在循环里先入栈左子树，后入栈右子树，循环结束后将结果逆序。

对于层序遍历的迭代实现，循环之前初始化一个有根节点的队列，此时队列只有一个元素，进入循环后，出队并访问，然后将根节点的左右子树依次入队。下次循环，依次将上次队列里的元素出队，同队入队他们的左右子树。这样每次循环只出队当前层次的节点，并入队他们的左右子树，完成了层次之间的交换。这实际上是一种广度优先搜索。层序遍历迭代写法：

# 层序遍历迭代，使用栈
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        q = [root]
        result = []
        while q:
            res = []
            for i in range(len(q)):
                node = q.pop(0)
                res.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            result.append(res)
        return result

# 层序遍历迭代，使用队列
from collections import deque
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []

        res = []
        q = deque()
        q.append(root)
        while q:
            size = len(q)
            curr_level = []
            for _ in range(size):
                node = q.popleft()
                curr_level.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            res.append(curr_level)
        return res

例题

二叉树的最近公共祖先

此题为leetcode第236题

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 树为空返回None
        if root is None:
            return None

        # 找到了p或q
        if root == p or root == q:
            return root

        # 在root的左子树找p或q
        left = self.lowestCommonAncestor(root.left, p, q)
        # 在root的右子树找p或q
        right = self.lowestCommonAncestor(root.right, p, q)

        if left is None:    # 如果左子树没有p或q，返回右孩子
            return right
        elif right is None: # 如果右子树没有p或q，返回左孩子
            return left
        else:               # 如果分别在左右子树找到了p或q，那么root就是最近公共祖先
            return root

总结

前序、中序、后序遍历的递归实现几乎一模一样，区别是根节点的访问位置不一样
前序、中序、后序的迭代实现需要借助栈
层序遍历的递归和迭代实现需要借助队列

访问统计

二叉树

二叉树遍历

前序遍历

中序遍历

后序遍历

层序遍历

程序实现

递归实现

迭代实现

例题

总结

发送评论编辑评论

二叉树

二叉树遍历

前序遍历

中序遍历

后序遍历

层序遍历

程序实现

递归实现

迭代实现

例题

总结

发送评论 编辑评论

推荐文章

发送评论编辑评论