自动化机器学习(AutoML)最近变得越来越火,是机器学习下个发展方向之一。其中的神经网络结构搜索(NAS)是其中重要的技术之一。人工设计网络需要丰富的经验和专业知识,神经网络有众多的超参数,导致其搜索空间巨大。NAS即是在此巨大的搜索空间里自动地找到最优的网络结构,实现深度学习的自动化。自2017年谷歌与MIT各自在ICLR上各自发表基于强化学习的NAS以来,已产出200多篇论文,仅2019年上半年就有100多篇论文。此系列文章将解读AutoDL领域的经典论文与方法,笔者也是刚接触这个领域,有理解错误的地方还请批评指正!
此篇博文介绍CMU的《DARTS:Differentiable Architecture Search》。之前介绍的NAS方法搜索空间都是离散的,而可微分方法将搜索空间松弛化使其变成连续的,则可以使用梯度的方法来解决。
一、DARTS:Differentiable Architecture Search
1、搜索空间
DARTS也是搜索卷积cell然后堆叠cell形成最终的网络。这里的cell是一个包含有向无环图,包含一个有$N$个节点的有序序列。每个节点$x^{(i)}$是一个隐含表示(比如特征图),每个有向的边$(i,j)$是变换$x^{(i)}$的操作$o^{(i,j)}$。作者假设cell有两个输入加点和一个输出节点,cell的输入输出设置和《Learning Transferable Architectures for Scalable Image Recognition》里的一致。每个中间节点是它所有的前驱节点计算得到:
$$x^{(i)}=sum_{j<i}o^{(i,j)}(x^{(j)})$$
一个特殊的操作:$zero$,包括在可能的操作集合里,表示两个节点之间没有连接。学习cell结构的任务就转换成了学习边上的操作。
2、松散化和优化
令$mathcal O$为可选操作的集合(比如卷积、最大池化、$zero$),每个操作表示作用在$x^{(i)}$上的函数$o(cdot)$。为了使搜索空间连续化,作者将特定操作的选择松弛化为在所有可能操作上的softmax:
$$ bar{o}^{(i, j)}(x)=sum{o in mathcal{O}} frac{exp left(alpha{o}^{(i, j)}right)}{sum{o^{prime} in mathcal{O}} exp left(alpha{o^{prime}}^{(i, j)}right)} o(x) $$
一对节点$(i,j)$之间的操作被一个$|mathcal O|$维向量$alpha^{(i,j)}$参数化。松弛化之后,搜索任务就变成了学习一组连续的变量${alpha} = {alpha^{(i,j)} }$,如下图所示:
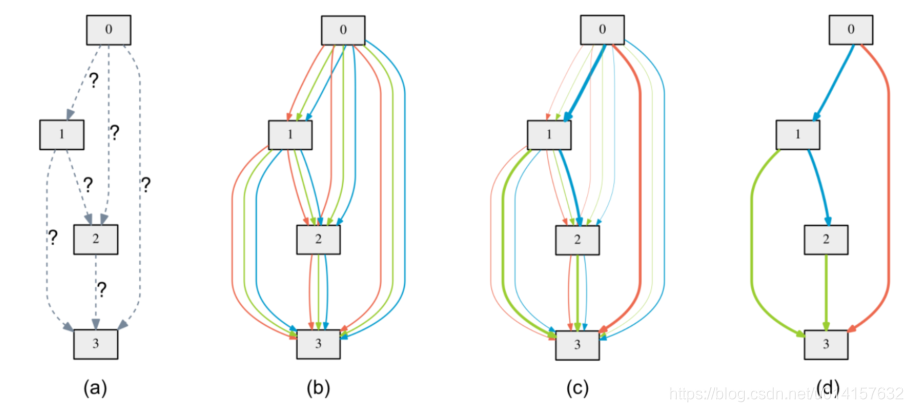
图(a)表示初始化的边,操作是未知的。图(b)通过在每条边放置混合的候选操作来松弛搜索空间,每个颜色的线表示不同的操作。图(c)是通过解决一个优化问题,联合训练候选操作的概率和网络的权重,不同的粗细表示了$alpha^{(i,j)}$的大小。图(d)是最终学习到的结构。
学习到了所有操作的可能性$bar{o}^{(i, j)}$后,选择其中最优可能的操作,也就是$o^{(i,j)}={rm argmax}{o in {mathcal O}}alpha{o}^{(i,j)}$。接下来,我们都用$alpha$表示结构。
松弛化之后,我们的目标就是共同地学习结构$alpha$和权重$w$,DARTS的目标是用梯度下降优化验证集损失。令$mathcal L{train}$和$mathcal L{val}$分别表示训练和验证损失,我们就是要找到一个最优的$alpha^{ast}$最小化验证集损失$mathcal L{val}(w^{ast},alpha^{ast})$,其中$w^{ast}$通过最小化训练集损失$mathcal L{train}(w,alpha^{ast})$。这是一个双层优化问题(bilevel opyimization problem),$alpha$是上层变量,$w$是下层变量:
$$ begin{align} begin{array}{cl}{min {alpha}} & {mathcal{L}{v a l}left(w^{}(alpha), alpharight)} tag1 {text { s.t. }} & {w^{}(alpha)=operatorname{argmin}{w} mathcal{L}{text {train}}(w, alpha)}end{array} end{align} $$
3、近似迭代求解优化问题
解决上面的双层优化问题是困难的,因为任何$alpha$的改变都会要求重新计算$w^{ast}(alpha)$。因此作者提出了一种近似的迭代解法,用梯度下降在权重空间和结构空间中轮流地优化$w$和$alpha$:

在第k步,给定当前结构$alpha{k-1}$,我们通过在最小化${mathcal L}{train}(w{k-1},alpha{k-1})$的方向上移动$w{k-1}$来获得$w{k}$。然后固定$w_{k}$,用单步梯度下降最小化验证集损失,以此更新结构:
$$ mathcal{L}{v a l}left(w{k}-xi nabla{w} mathcal{L}{t r a i n}left(w{k}, alpha{k-1}right), alpha_{k-1}right) tag2 $$
其中$xi$是学习率。通过求用式(2)关于$alpha$的导数得到结构梯度(为了简介,省略了角标k):
$$ nabla{alpha} mathcal{L}{v a l}left(w^{prime}, alpharight)-xi nabla{alpha, w}^{2} mathcal{L}{t r a i n}(w, alpha) nabla{w^{prime}} mathcal{L}{v a l}left(w^{prime}, alpharight) tag3 $$
其中$w^{prime}=w-xi nabla{w} mathcal{L}{t r a i n}(w, alpha)$。上式第二项包含了矩阵向量乘积,难以计算。不过使用有限差分近似可以大大降低复杂度,令$epsilon$是一个很小的数,$w^{+}=w+epsilon nabla{w^{prime}} mathcal{L}{v a l}left(w^{prime}, alpharight)$ ,$w^{-}=w-epsilon nabla{w^{prime}} mathcal{L}{v a l}left(w^{prime}, alpharight)$,那么:
$$ nabla{alpha, w}^{2} mathcal{L}{t r a i n}(w, alpha) nabla{w^{prime}} mathcal{L}{v a l}left(w^{prime}, alpharight) approx frac{nabla{alpha} mathcal{L}{t r a i n}left(w^{+}, alpharight)-nabla{alpha} mathcal{L}{t r a i n}left(w^{-}, alpharight)}{2 epsilon} tag4 $$
当$epsilon=0$时,式(3)的二阶导数消失,结构梯度仅由$nabla{alpha} mathcal{L}{v a l}(w, alpha)$提供,通过假设$alpha$和$w$相互独立来启发式地最优化验证集损失。这会加速计算,但通过实验发现效果并不好。因此要选择一个合适的$epsilon$值。作者称$epsilon=0$的情况为一阶近似,$epsilon>0$为二阶近似
参考文献
[1] Liu, Hanxiao, Karen Simonyan, and Yiming Yang. "Darts: Differentiable architecture search." arXiv preprint arXiv:1806.09055 (2018). [2] 《深度理解AutoML和AutoDL》